Visit TS200 Page

Visit TS250 Page

Ask Us Questions

Request a Quote

Instruments For Testing Your Innovations

Magnetic Coil Cutoff Frequency Calculation For Current Source

There are application cases where current source is desirable. Current source is useful for maintaining constant current amplitude while the load impedance is change over frequency (or voltage or temperature). A perfect example is producing fixed AC magnetic field (constant current) over a frequency range. When using current source, the frequency response is very different from that of the traditional voltage-source. The 3dB cutoff frequency in analog circuits is well understood when using voltage-source. An example is the simple RC circuit cutoff (corner) frequency is f3dB = 1/(2πRC).

The cutoff frequencies of analog circuits for current source is different from that of voltage source. Figure 1 shows a simplified current-output driver/amplifier. It has a current output, while the input is voltage from a signal generator for example. The high current driver is therefore equivalent to a voltage-controlled-current-source. Below is the derivation for the cutoff frequency for a current source. All of the equations applied to the voltage and current at the output of the driver.

The voltage across a load is governed by Ohm's law giving in Equation 1. The I is the current, the Z is the impedance. For an inductive load such as AC magnetic coils, whose impedance is jωL. ω is the angular frequency or 2πf, and L is the inductance. Since we are calculating the magnitude, we will ignore the phase j. Equation 1 becomes Equation 2 for an inductive load such as Helmholtz coil set for example. Since ω = 2πf, Equation 3 is the voltage across the inductive load. Rearrange Equation 3 to solve for the frequency and the result is shown in Equation 4.

The current source driver has limited voltage range (compliance voltage range), and it also has a maximum output current limit (compliance current range). After inserting the maximum voltage and the desired set current, the maximum frequency without limited by voltage is given in Equation 5. This is also called the dropout frequency. ISet is set current or the regulated current at low-frequency.

Table 1. Magnetic Coil Driver Selection Guide

Helmholtz Coil Pair For Producing Uniform Field

Calculating Magnetic Field for Solenoid and Coil

Strong Magneti Field Using a Current-Boost Resonant

Series Resonant Generate Strong Magnetic Field

High-Frequency Magnetic Coil Design Resources

Visit TS200 Product Page

TS250 vs. TS200

Visit TS250 Product Page

Ask Us Questions

Request a Quote

Quick Links

Related Technical Information

PDF Version of this App Note

TS250 Price List

TS200 Price List

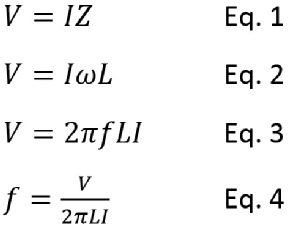
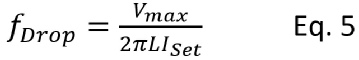
Any higher frequency than the dropout frequency will cause current to go out-of-regulation. The driver's output current will be reduced at higher frequency. This is because the driver's output voltage has reached its maximum. For example, for an AC solenoid coil current driver that can output a maximum of 30V, the set output current of 1A, and the total coil inductance of 10mH, the dropout frequency is 477Hz. Any higher frequency will cause the current to reduce. Note the dropout frequency is a function of set output current. Lower current will have higher dropout frequency.

At the dropout frequency, the current is still output at 100% of the set current. The traditional corner (3dB) frequency definition for a voltage source is when the frequency reach to a point where output voltage is reduced by a factor of 1/√2 or about 0.707 of the "expected" value. To use this definition and apply to a current source driver, Equation 3 is reused as shown in Equation 6. Equation-6 is then rearranged to solve for the current as a function of frequency and the result is shown in Eq-7. Equation-7 is valid for frequency is higher than the dropout frequency when the current is out-of-regulation.

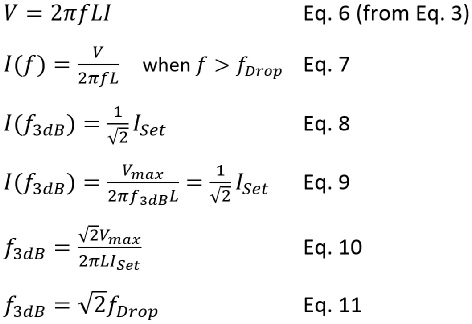
Equation 8 is setup to solve the cutoff (-3dB) frequency at which the current is 1/√2 of the set current. Substitute Equation-7 into the left-side of Eq-8 yields Equation 9. Rearrange Equation-9 to obtain Eq-10 for the 3dB cutoff frequency. Compared Equation 10 and 5, the 3dB cutoff frequency can be written in term of the dropout frequency as in Eq. 11. Again, using the example of 10mH Helmholtz coil and 30V and 1A current source, the 3dB cutoff frequency is 675Hz.

The above equations and discussions are for inductors (electromagnetic coils, solenoids, Helmholtz coils, relays, motors, etc.). Plotting Eq-7 in Figure 2 shows the current source transfer function is a low-pass filter. The coil inductance is acting as a filtering element. In a similar way the frequency response of capacitive devices such as piezoelectric transducers and actuators can be derived. Capacitive device frequency response is a high-pass filter to be discussed here in another application note.

In conclusion, this application note shows that for current-source there is a "dropout" frequency that traditional voltage-source circuit is lacking. The dropout frequency is when the current-source or the driver has reach the maximum voltage. As the frequency is going higher, the current is out-of-regulation and reduced in amplitude. When the current amplitude is reduced to the -3dB level, this is the cutoff frequency as expressed in Eq. 10.

The voltage across a load is governed by Ohm's law giving in Equation 1. The I is the current, the Z is the impedance. For an inductive load such as AC magnetic coils, whose impedance is jωL. ω is the angular frequency or 2πf, and L is the inductance. Since we are calculating the magnitude, we will ignore the phase j. Equation 1 becomes Equation 2 for an inductive load such as Helmholtz coil pair for example. Since ω = 2πf, Equation 3 is the voltage across the inductive load. Rearrange Equation 3 to solve for the frequency and the result is shown in Equation 4.

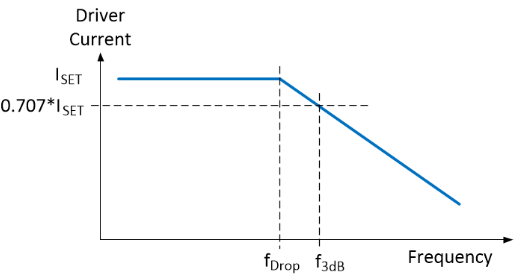
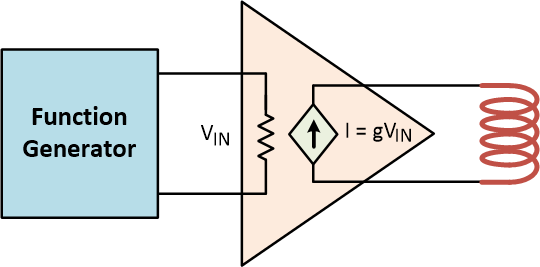
Figure 1. Constant output current driver for driving electromagnetic coil.

Figure 2. Inductive coil frequency response with constant-current driver.